[dreamhack] level 1 아 문제 이름 뭘로하지 문제 풀이..

 

ida로 디컴파일 해보니 사용자에게 입력을 받고, s를 파라미터로 하는 함수인 sub_145A의 값이 참이면 correct 출력, 아니라면 wrong을 출력한다. 해당 문제는 어떤 값을 입력해야 correct가 나오는지 알아내야 하는 문제 같다. 

sub_145A 함수 분석

만약 input 값의 길이가 39가 아니라면 0을 반환

v2~v7 : 순서대로 input + 8, 24, 32, 36, 38을 연산한 값을 저장

s1[0~3] : 순서대로 Input,  v2, input + 16, v3를 저장

sub_1273 함수 호출

sub_139D 함수 호출

s1과 s2의 첫 0x27 바이트를 비교하여 결과가 0이라면 참(1)을 반환하고 아니라면 거짓(2)를 반환.

 

** main 함수에서 correct가 나오려면 memcmp 비교 결과가 0이어야 함. **

 

sub_1273 함수 분석

1바이트씩 해석함. 만약 i가 0x27보다 크거나 같으면 break

byte_2020[(unsigned __int8)(((-83 - (i & 7)) * ((i & 7) - 34)) ^ i)] + (*(_BYTE *)(s1 + i) ^ (unsigned __int8)(i + (-83 - (i & 7)) * ((i & 7) - 34))), (unsigned __int8)(i % 7) + 3 의 연산값을 인자로 하는 sub_123E 함수의 반환값을 v2에 저장 

 

unsigned char ida_chars[] =

{

99, 124, 119, 123, 242, 107, 111, 197, 48, 1,

103, 43, 254, 215, 171, 118, 202, 130, 201, 125,

250, 89, 71, 240, 173, 212, 162, 175, 156, 164,

114, 192, 183, 253, 147, 38, 54, 63, 247, 204,

52, 165, 229, 241, 113, 216, 49, 21, 4, 199,

35, 195, 24, 150, 5, 154, 7, 18, 128, 226,

235, 39, 178, 117, 9, 131, 44, 26, 27, 110,

90, 160, 82, 59, 214, 179, 41, 227, 47, 132,

83, 209, 0, 237, 32, 252, 177, 91, 106, 203,

190, 57, 74, 76, 88, 207, 208, 239, 170, 251,

67, 77, 51, 133, 69, 249, 2, 127, 80, 60,

159, 168, 81, 163, 64, 143, 146, 157, 56, 245,

188, 182, 218, 33, 16, 255, 243, 210, 205, 12,

19, 236, 95, 151, 68, 23, 196, 167, 126, 61,

100, 93, 25, 115, 96, 129, 79, 220, 34, 42,

144, 136, 70, 238, 184, 20, 222, 94, 11, 219,

224, 50, 58, 10, 73, 6, 36, 92, 194, 211,

172, 98, 145, 149, 228, 121, 231, 200, 55, 109,

141, 213, 78, 169, 108, 86, 244, 234, 101, 122,

174, 8, 186, 120, 37, 46, 28, 166, 180, 198,

232, 221, 116, 31, 75, 189, 139, 138, 112, 62,

181, 102, 72, 3, 246, 14, 97, 53, 87, 185,

134, 193, 29, 158, 225, 248, 152, 17, 105, 217,

142, 148, 155, 30, 135, 233, 206, 85, 40, 223,

140, 161, 137, 13, 191, 230, 66, 104, 65, 153,

45, 15, 176, 84, 187, 22

};

 

sub_123E 함수 분석

해당 함수는 a1, a2에 대해. 비트 쉬프트 연산을 한다.

 

sub_139D 함수 분석

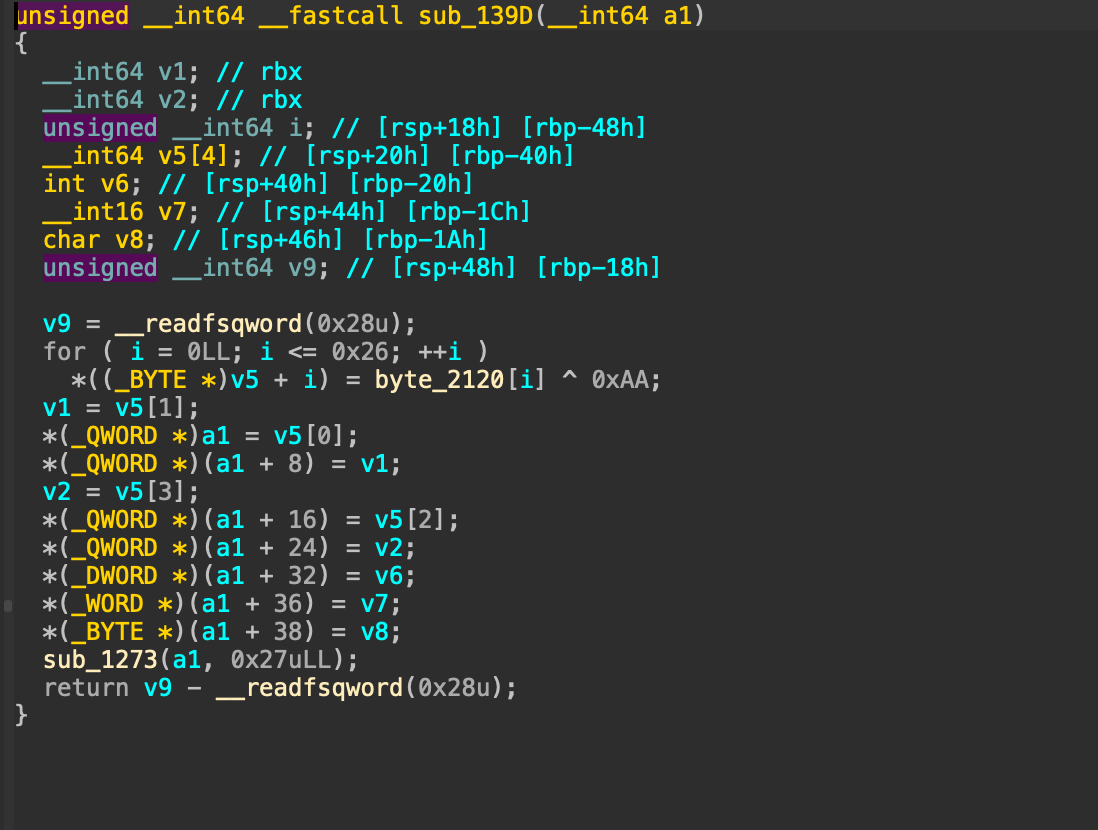
0x26만큼 반복하고 특정 연산을 한 뒤에 sub_1273 함수를 실행한다. 그리고 v9 - _readfsqword 연산을 수행한 값을 반환한다.

 

unsigned char ida_chars[] =

{

238, 226, 209, 250, 198, 207, 203, 217, 207, 245,

198, 197, 220, 207, 245, 222, 194, 207, 245, 237,

238, 245, 255, 232, 239, 248, 231, 239, 249, 226,

245, 203, 198, 200, 223, 199, 139, 139, 215

};

 

위의 함수들을 활용하여 모두 역연산하면 될 것 같다. 

 

역연산 코드

def rotate_right(value, amount):
    """Rotate bits to the right (equivalent to sub_123E)
    Handles negative shift counts by converting to positive"""
    # Ensure amount is positive and within range
    amount = amount % 8
    return ((value >> amount) | (value << (8 - amount))) & 0xFF


def rotate_left(value, amount):
    """Rotate bits to the left (inverse of sub_123E)
    Handles negative shift counts by converting to positive"""
    # Ensure amount is positive and within range
    amount = amount % 8
    return ((value << amount) | (value >> (8 - amount))) & 0xFF


# S-box from the disassembly
byte_2020 = [
    99, 124, 119, 123, 242, 107, 111, 197, 48, 1,
    103, 43, 254, 215, 171, 118, 202, 130, 201, 125,
    250, 89, 71, 240, 173, 212, 162, 175, 156, 164,
    114, 192, 183, 253, 147, 38, 54, 63, 247, 204,
    52, 165, 229, 241, 113, 216, 49, 21, 4, 199,
    35, 195, 24, 150, 5, 154, 7, 18, 128, 226,
    235, 39, 178, 117, 9, 131, 44, 26, 27, 110,
    90, 160, 82, 59, 214, 179, 41, 227, 47, 132,
    83, 209, 0, 237, 32, 252, 177, 91, 106, 203,
    190, 57, 74, 76, 88, 207, 208, 239, 170, 251,
    67, 77, 51, 133, 69, 249, 2, 127, 80, 60,
    159, 168, 81, 163, 64, 143, 146, 157, 56, 245,
    188, 182, 218, 33, 16, 255, 243, 210, 205, 12,
    19, 236, 95, 151, 68, 23, 196, 167, 126, 61,
    100, 93, 25, 115, 96, 129, 79, 220, 34, 42,
    144, 136, 70, 238, 184, 20, 222, 94, 11, 219,
    224, 50, 58, 10, 73, 6, 36, 92, 194, 211,
    172, 98, 145, 149, 228, 121, 231, 200, 55, 109,
    141, 213, 78, 169, 108, 86, 244, 234, 101, 122,
    174, 8, 186, 120, 37, 46, 28, 166, 180, 198,
    232, 221, 116, 31, 75, 189, 139, 138, 112, 62,
    181, 102, 72, 3, 246, 14, 97, 53, 87, 185,
    134, 193, 29, 158, 225, 248, 152, 17, 105, 217,
    142, 148, 155, 30, 135, 233, 206, 85, 40, 223,
    140, 161, 137, 13, 191, 230, 66, 104, 65, 153,
    45, 15, 176, 84, 187, 22
]

# Target bytes from the disassembly
byte_2120 = [
    238, 226, 209, 250, 198, 207, 203, 217, 207, 245,
    198, 197, 220, 207, 245, 222, 194, 207, 245, 237,
    238, 245, 255, 232, 239, 248, 231, 239, 249, 226,
    245, 203, 198, 200, 223, 199, 139, 139, 215
]


def sub_123E(a1, a2):
    """Implementation of the sub_123E function according to the disassembly

    Based on the assembly, this seems to be a right rotate:
    return ((a1 >> a2) | (a1 << (8 - a2))) & 0xFF

    But looking at the disassembly, it might actually be different.
    Let's check the original code:
    ```
    __int64 __fastcall sub_123E(unsigned __int8 a1, char a2)
    {
      return ((int)a1 >> a2) | (a1 << (8 - a2));
    }
    ```

    This seems to be a rotate right, but let's verify it's a right rotate.
    """
    # Ensure a2 is a valid positive shift amount
    a2 = a2 & 0x7  # Same as a2 % 8, but faster
    return ((a1 >> a2) | (a1 << (8 - a2))) & 0xFF


def calculate_xor_value(i):
    """Calculate the XOR value used in sub_1273
    This needs to match the assembly's computation exactly"""
    # The assembly code: (-83 - (i & 7)) * ((i & 7) - 34)
    # We need to make sure this matches the binary's computation

    # Ensure we're doing the computation exactly as in the binary
    term1 = (-83 - (i & 7)) & 0xFF  # Keep in byte range
    term2 = ((i & 7) - 34) & 0xFF  # Keep in byte range
    result = (term1 * term2) & 0xFF  # Multiplication can overflow, so mask
    return (result ^ i) & 0xFF


def sub_1273(s1, length):
    """Properly implemented sub_1273 function with correct byte range handling"""
    v4 = 0

    for i in range(length):
        # Calculate the index into byte_2020
        xor_value = calculate_xor_value(i)
        index = xor_value & 0xFF

        # Ensure index is in valid range
        index = index % len(byte_2020)

        # Get value from byte_2020 and calculate
        sbox_value = byte_2020[index]
        input_byte = s1[i]
        i_plus_xor = (i + xor_value) & 0xFF
        sum_value = (sbox_value + (input_byte ^ i_plus_xor)) & 0xFF

        # Rotate the bits
        rot_amount = (i % 7) + 3
        v2 = sub_123E(sum_value, rot_amount)

        # Update the current byte and v4
        new_byte = ((i + v4) ^ ((3 * v2 + 7) & 0xFF)) & 0xFF
        s1[i] = new_byte
        v4 = new_byte

    return length


def reverse_sub_1273(encrypted, length):
    """Reverse the transformations of sub_1273"""
    original = bytearray(length)
    v4 = 0

    for i in range(length):
        # Extract the current encrypted byte
        encrypted_byte = encrypted[i]

        # Recover what v2 would have been using the relationship:
        # encrypted_byte = (i + v4) ^ (3 * v2 + 7)
        v4_contribution = (i + v4) & 0xFF
        target = (v4_contribution ^ encrypted_byte) & 0xFF

        # Find v2 such that (3 * v2 + 7) & 0xFF == target
        v2 = None
        for test_v2 in range(256):
            if ((3 * test_v2 + 7) & 0xFF) == target:
                v2 = test_v2
                break

        if v2 is None:
            raise ValueError(f"Could not find v2 for position {i}")

        # Undo the rotation
        rot_amount = (i % 7) + 3
        # For rotate right with amount 'a', the inverse is rotate left with amount 'a'
        unrotated = rotate_left(v2, rot_amount)

        # Calculate the XOR value used in the original function
        xor_value = calculate_xor_value(i)

        # Find the sbox value
        index = xor_value & 0xFF
        index %= len(byte_2020)
        sbox_value = byte_2020[index]

        # Recover the original input byte
        # We had: sum_value = (sbox_value + (input_byte ^ (i + xor_value))) & 0xFF
        # And: unrotated = sum_value
        # So: input_byte = (unrotated - sbox_value) ^ (i + xor_value)
        i_plus_xor = (i + xor_value) & 0xFF
        original_byte = ((unrotated - sbox_value) & 0xFF) ^ i_plus_xor
        original[i] = original_byte

        # Update v4 for the next iteration
        v4 = encrypted_byte

    return original


def main():
    """Main function to recover the flag"""
    # First, XOR byte_2120 with 0xAA as done in sub_139D
    expected = bytearray(39)
    for i in range(39):
        expected[i] = byte_2120[i] ^ 0xAA

    # Create a copy for processing
    processed = bytearray(expected)

    # Apply sub_1273 to see what should match in the memcmp
    sub_1273(processed, 0x27)

    # Now reverse the process to get the original flag
    flag_bytes = reverse_sub_1273(processed, 0x27)

    # Convert to ASCII and print
    flag = ''.join(chr(b) for b in flag_bytes)
    print("Recovered flag:", flag)

    # Verify our implementation is correct by applying sub_1273 to flag_bytes
    verification = bytearray(flag_bytes)
    sub_1273(verification, 0x27)

    # This should match the processed buffer
    if verification == processed:
        print("Verification successful - our implementation is correct!")
    else:
        print("Verification failed - our implementation might be incorrect")


if __name__ == "__main__":
    main()

 

flag : DH{Please_love_the_GD_UBERMESH_album!!}